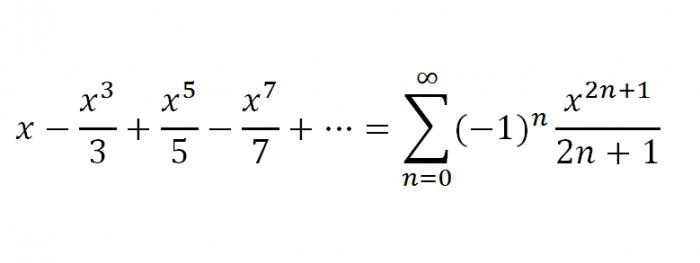एक समारोह के शून्य और उन्हें परिभाषित करने के लिए क्या हैं?
एक समारोह के शून्य क्या हैं? जवाब बहुत सरल है - यह एक गणितीय शब्द है, जिसके द्वारा किसी दिए गए फ़ंक्शन की परिभाषा का डोमेन है, जिस पर इसका मान शून्य है। एक समारोह के शून्य को समीकरण की जड़ों भी कहा जाता है। कुछ सरल उदाहरणों पर, फ़ंक्शन के शून्यों को स्पष्ट करने का सबसे आसान तरीका है।
उदाहरण
सरल समीकरण वाई = एक्स + 3 पर विचार करें। चूंकि फ़ंक्शन का शून्य उस तर्क का मान है जिस पर y ने शून्य मान प्राप्त किया है, समीकरण के बाईं ओर 0 को प्रतिस्थापित करें:
0 = एक्स + 3;
एक्स = -3।
इस मामले में, -3 वांछित शून्य है। इस समारोह के लिए, समीकरण का केवल एक जड़ है, लेकिन यह हमेशा मामला नहीं है।
चलिए एक और उदाहरण मानते हैं:
वाई = एक्स2-9.
हम समीकरण के बाईं तरफ 0 को प्रतिस्थापित करते हैं, जैसा कि पिछले उदाहरण में है:
0 = एक्स2-9;
-9 = एक्स2 .
यह स्पष्ट है कि इस मामले में समारोह के शून्य होंगेदो: एक्स = 3 और एक्स = -3। यदि समीकरण में तीसरी डिग्री का तर्क था, तो तीन शून्य होंगे। कोई एक साधारण निष्कर्ष निकाल सकता है कि बहुपद की जड़ों की संख्या समीकरण में समीकरण की अधिकतम डिग्री से मेल खाती है। हालांकि, कई कार्यों, उदाहरण के लिए वाई = एक्स3 , पहली नज़र में इस कथन का खंडन करते हैं। तर्क और सामान्य ज्ञान का सुझाव है कि इस फ़ंक्शन में बिंदु x = 0 पर केवल एक शून्य है। लेकिन वास्तव में तीन जड़ें हैं, वे सब सिर्फ मेल खाते हैं। यदि समीकरण एक जटिल रूप में हल किया जाता है, तो यह स्पष्ट हो जाता है। x = 0 इस मामले में, जिस रूट की बहुतायत 3 है। पिछले उदाहरण में, शून्य मेल नहीं खाए, इसलिए उनके पास बहुतायत 1 थी।

निर्धारण के लिए एल्गोरिदम
प्रस्तुत उदाहरणों से, आप देख सकते हैं कि फ़ंक्शन के शून्य को कैसे निर्धारित किया जाए। एल्गोरिदम हमेशा एक जैसा होता है:
- एक समारोह लिखें।
- वाई या एफ (x) = 0 का स्थान बदलें।
- परिणामी समीकरण हल करें।
अंतिम वस्तु की जटिलता डिग्री पर निर्भर करती हैसमीकरण का तर्क। उच्च-डिग्री समीकरणों को हल करते समय, यह याद रखना महत्वपूर्ण है कि समीकरण की जड़ों की संख्या तर्क की अधिकतम शक्ति के बराबर है। यह त्रिकोणमितीय समीकरणों के लिए विशेष रूप से सच है, जहां साइन या कोसाइन द्वारा दोनों हिस्सों को विभाजित करने से जड़ों की हानि होती है।
मनमानी डिग्री के समीकरणों को गोर्नर विधि द्वारा आसानी से हल किया जाता है, जिसे विशेष रूप से मनमाने ढंग से बहुपद के शून्य खोजने के लिए विकसित किया गया था।
कार्यों के शून्य का अर्थ या तो हो सकता हैजटिल, और सकारात्मक, असली या जटिल विमान, एकल या एकाधिक में झूठ बोल रहा है। या समीकरण की जड़ें नहीं हो सकती हैं। उदाहरण के लिए, फ़ंक्शन y = 8 को किसी भी x के लिए शून्य मान नहीं मिलेगा, क्योंकि यह इस चर पर निर्भर नहीं है।
समीकरण वाई = एक्स2-16 में दो जड़ों हैं, और दोनों जटिल विमान में झूठ बोलते हैं: एक्स1= 4i, एक्स2= -4 ई।
सामान्य गलतियाँ
एक आम गलती है कि स्कूली बच्चों की अनुमति है, अभी भीवास्तव में समझ में नहीं आता कि फ़ंक्शन के शून्य क्या हैं, तर्क के अनुसार तर्क (x) का प्रतिस्थापन है, और फ़ंक्शन का मान (y) नहीं है। वे निश्चित रूप से समीकरण x = 0 में प्रतिस्थापित हैं और, इस पर आधारित, y पाया जाता है। लेकिन यह एक गलत दृष्टिकोण है।
एक और गलती, जैसा कि पहले से ही उल्लेख किया गया है,ट्रायोनोमेट्रिक समीकरण में साइन या कोसाइन, जिसके कारण फ़ंक्शन का एक या अधिक शून्य खो जाता है। इसका मतलब यह नहीं है कि इस तरह के समीकरणों में कुछ भी कम नहीं किया जा सकता है, केवल आगे की गणना के साथ इन "खोए" कारकों को ध्यान में रखना आवश्यक है।
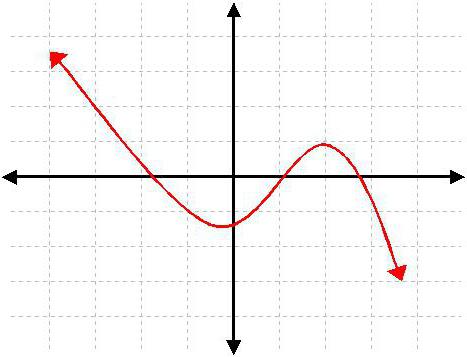
ग्राफिकल प्रतिनिधित्व
यह समझने के लिए कि फ़ंक्शन के शून्य क्या हैं, आप इसका उपयोग कर सकते हैंइस तरह के मेपल के रूप में गणितीय कार्यक्रम। यह एक ग्राफ अंक की वांछित संख्या और वांछित पैमाने का संकेत निर्माण संभव है। उन बिंदुओं जिस पर ग्राफ पार करती x- अक्ष आवश्यक शून्य है। यह एक बहुपद की जड़ों की खोज है, खासकर अगर यह तीसरे क्रम की तुलना में अधिक है का सबसे तेजी से तरीकों में से एक है। तो अगर नियमित रूप से गणितीय गणना मनमाना शक्तियों का बहुआयामी पद की जड़ों को खोजने के लिए प्रदर्शन करने के लिए,, कार्यक्रम निर्माण की आवश्यकता है, मेपल या इसी तरह के कार्यक्रम बस कार्यान्वयन और गणना के सत्यापन के लिए अपरिहार्य है।